Faktorial Anova

Faktorial ANOVA menguji perbedaan mean antar kelompok data berdasarkan pada dua atau lebih variabel independen, dengan variabel dependen tunggal. Faktorial ANOVA dapat melibatkan dua atau lebih data kategorik/ordinal antar subjek atau satu data interval atau rasio.Faktorial ANOVA digunakan ketika kita ingin mempertimbangkan efek lebih dari satu faktor pada perbedaan dalam variabel dependen. Sebuah rancangan faktorial adalah desain eksperimental di mana setiap tingkat masing-masing faktor dipasangkan atau disilangkan dengan tiap tingkat setiap faktor lainnya. Dengan kata lain setiap kombinasi dari faktor-faktor tingkat disertakan dalam desain. Desain jenis ini sering digambarkan dalam sebuah tabel matriks (misal 2 x 3, dll). 

Desain faktorial memungkinkan kita untuk menentukan apakah ada interaksi antara variabel bebas atau faktor yang dipertimbangkan. Interaksi menyiratkan bahwa perbedaan dalam salah satu faktor perbedaan tergantung pada faktor lain.

Ilustrasi

Faktorial ANOVA dapat digunakan jika kita ingin mengetahui apakah jenis kelamin (pria/wanita) dan tingkat pendapatan (tinggi/rendah) mempengaruhi keputusan pembelian makanan fastfood. Data konsumsi fastfood dinyatakan dalam frekuensi kunjungan setiap tahun. Data yang diberikan adalah sebagai berikut:

Gambar 1. Contoh Faktorial ANOVA

Dari ilustrasi tersebut, hipotesis yang akan kita gunakan adalah:
H01 : tidak ada perbedaan yang signifikan antara tingkat pendapatan tinggi dan rendah 
H02 : tidak ada perbedaan yang signifikan antara jenis kelamin pria dan wanita
H03 : tidak terjadi efek interaksi antara jenis kelamin dan jenis pekerjaan terhadap frekuensi kunjungan.

Dengan SPSS 17.0 langkah-langkahnya dapat kita lakukan sebagai berikut:

1. Input data ke dalam worksheet SPSS seperti berikut:





Gambar 2. Input Data Konsumsi Fastfood


2. Setelah muncul kotak dialog Univariate, maka pindahkan variabel yang akan diukur (frekuensi) ke dalam kotak dependent variable dan variabel sex dan income ke dalam kotak fixed factor:





Gambar 3. Kotak Dialog Univariate


3. Pilih pada menubar Analyze – General Linear Model – Univariate seperti berikut:





Gambar 4. Analyze – General Linear Model – Univariate


4. Kemudian klik continue, pilih plots, masukkan variabel kategori sex dan income masing-masing ke dalam kotak horizontal axis dan separate lines seperti berikut: kemudian klik add – continue,





Gambar 5. Plots Variabel Kategori Sex dan Income


5. Setelah itu pilih option, masukkan variabel sex, income, dan sex*income ke dalam kotak kotak displays mean for, lalu centang descriptive statistic, observed power, dan homogeneity test seperti berikut:





Gambar 6. Kotak Dialog displays mean for


6. Setelah itu klik continue dan OK, maka akan ditunjukkan output berikut:





Gambar 7. Output Faktorial Anova 

Dari output descriptive statistics dapat kita lihat nilai mean dan standard deviasi masing-masing variabel dan totalnya.

Gambar 8. Levene’s Test of Equality

Dari output Levene’s Test of Equality kita dapat mengetahui signifikansi model adalah sebesar 0,065 (0,065 > 0,05), maka kita simpulkan bahwa keragaman berbeda signifikan dan model tidak homogen.

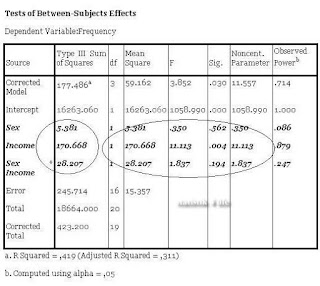
Gambar 9. Tests of Between Subjects Effects

Dari output dependent variable: Frequency dapat kita lihat bahwa efek Sex dan Interaksi variabel Sex*Income memiliki nilai p-value (sig. > 0,05) berarti bahwa tidak ada interaksi yang signifikan antara variabel Sex dan Income dalam hubungannya terhadap frekuensi kunjungan ke gerai fastfood. Efek yang signifikan terhadap frekuensi kunjungan hanya Income dengan nilai p-value (sig. < 0,05), ini menunjukkan bahwa tingkat pendapatan berpengaruh signifikan terhadap kunjungan ke gerai fastfood. Sedangkan Sex tidak menunjukkan signifikansi yang mempengaruhi kunjungan dengan nilai p-value = 0,562 (0,562 > 0,05).

Gambar 10. Plots Estimated marginal Means of Frequency

Plot yang didapat tidak menunjukkan adanya interaksi hubungan antara jenis kelamin (sex) dengan tingkat pendapatan (income) yang mempengaruhi kunjungan ke gerai fastfood, karena garis tidak bertemu (berinteraksi).